As described in the class contents above, interspersed throughout the class we will study stochastic systems that arise in different disciplines. In the last 30 years or so we have come to realize that randomness is a fundamental property of systems. Therefore, much of systems’ analysis that used to be done assuming deterministic behavior is nowadays done from a stochastic systems purview.
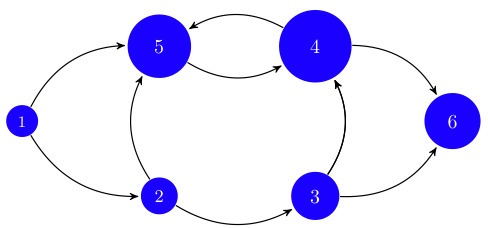
The first application concerns the problem of ranking elements of a network that arises in social sciences as well as in computer science. The idea is to associate importance of a node with its degree of connectivity. However, it is not only a matter of counting the number of links to a node, but also of pondering the importance of the nodes that point to it, see Fig. 1. An elegant solution to this problem is a stochastic algorithm based on a random walk through elements of the network. The best known uses of this algorithm are Google’s PageRank that ranks web pages returned by Google searches and the categorization of scientific papers. This algorithm will be covered in class and in Homework 6.
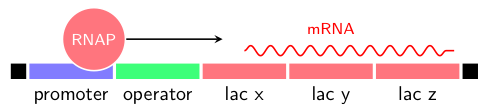
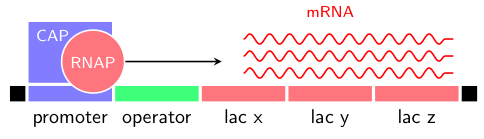
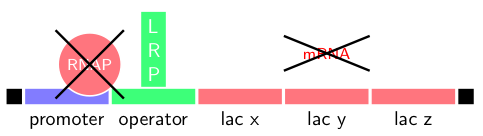
We will also consider simulation and modeling of biochemical reactions that are characterized by the involvement of a small number of reactants. In such cases it is known that randomness may play an important role in the overall behavior of the system. Gillespie’s algorithm is the workhorse technique that will be covered in class along with representative examples. In Homework 10 you will use this algorithm to study the gene autoregulatory network that controls the digestion of lactose; see Fig. 2.
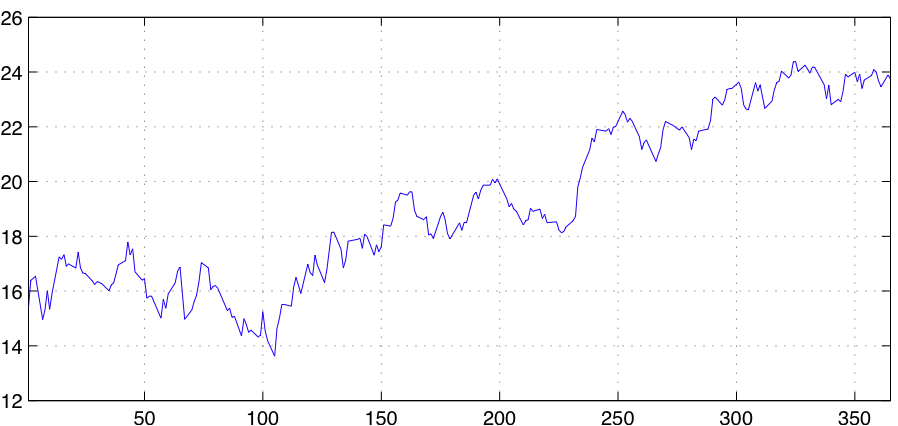
The last example covered in class comes from financial engineering, namely the Black–Scholes model for option pricing. A look at Fig. 3 is enough to realize that randomness plays a role in the price of stocks. Empirically, it has been observed that stock prices can be modeled as a geometric Brownian motion. This fact and the concept of arbitrage, that is, the opportunity to realize a benefit without risk, permit introduction of the risk neutral measure. Black-Scholes formula for option pricing, as well as the pricing of derivatives in general, is a simple application of the risk neutral measure. In Homework 13 you will use the risk neutral measure to price an option on Cisco’s stock.
There are many other examples that could be studied, and we are indeed, considering many more in the homework assignments. You are invited to take a look.
